Grundlagen der Wahrscheinlichkeitsrechnung

Entdecke die grundlegenden Konzepte der Wahrscheinlichkeitsrechnung und lerne, wie du Baumdiagramme zur Lösung von Wahrscheinlichkeitsproblemen einsetzt.

Die Basics der Wahrscheinlichkeitsrechnung

In der Wahrscheinlichkeitsrechnung geht es darum, die Chancen für das Eintreten bestimmter Ereignisse zu bestimmen. Hier lernst du die grundlegenden Konzepte und wie man mit Baumdiagrammen arbeitet.

Grundlegende Wahrscheinlichkeitsbegriffe

Bevor wir uns mit Baumdiagrammen beschäftigen, sollten wir die wichtigsten Begriffe der Wahrscheinlichkeitsrechnung verstehen.

Grundbegriffe

Wichtige Begriffe

Zufallsexperiment: Ein Vorgang mit zufälligem Ausgang (z.B. Würfeln, Münzwurf).
Ergebnis: Ein möglicher Ausgang eines Zufallsexperiments.
Ergebnismenge Ω: Die Menge aller möglichen Ergebnisse eines Zufallsexperiments.
Ereignis: Eine Teilmenge der Ergebnismenge (z.B. "gerade Augenzahl beim Würfeln").
Wahrscheinlichkeit P(A): Eine Zahl zwischen 0 und 1, die angibt, wie wahrscheinlich das Eintreten eines Ereignisses A ist.

Berechnung von Wahrscheinlichkeiten

Bei Laplace-Experimenten (alle Ergebnisse sind gleich wahrscheinlich) berechnet man die Wahrscheinlichkeit so:

$$P(A) = \frac{\text{Anzahl der für A günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}}$$

Beispiel: Würfelwurf

Beim Werfen eines Würfels gibt es 6 mögliche Ergebnisse: {1, 2, 3, 4, 5, 6}.

Die Wahrscheinlichkeit, eine gerade Zahl zu würfeln, beträgt:

$$P(\text{gerade Zahl}) = \frac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl aller Ergebnisse}} = \frac{3}{6} = \frac{1}{2} = 0,5 = 50\%$$

Baumdiagramme

Baumdiagramme sind ein mächtiges Werkzeug, um mehrstufige Zufallsexperimente zu visualisieren und Wahrscheinlichkeiten zu berechnen.

Was ist ein Baumdiagramm?

Ein Baumdiagramm ist eine grafische Darstellung von aufeinanderfolgenden Ereignissen. Jeder "Ast" des Baums repräsentiert ein mögliches Ergebnis, und an jedem Ast steht die zugehörige Wahrscheinlichkeit.

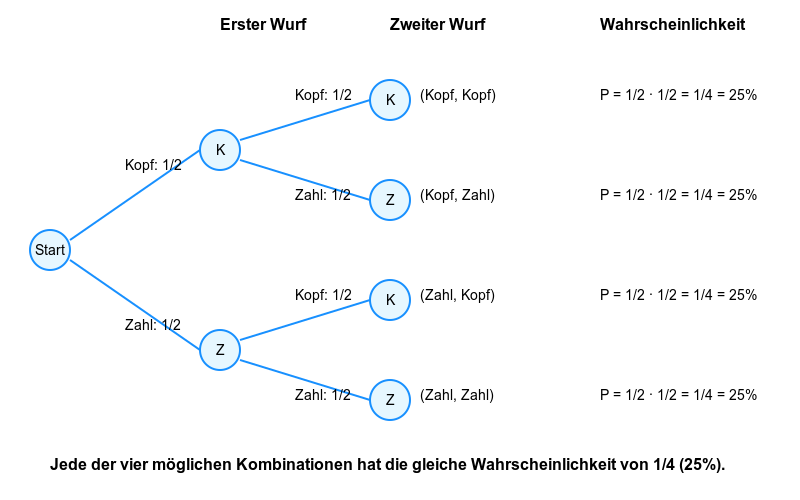
Einfaches Baumdiagramm für einen Münzwurf und anschließenden Würfelwurf

Aufbau eines Baumdiagramms

Knoten: Stellt einen Punkt im Zufallsexperiment dar, an dem verschiedene Ergebnisse möglich sind.
Äste/Kanten: Verbindungen zwischen Knoten, die mögliche Ergebnisse repräsentieren.
Wahrscheinlichkeiten: An jedem Ast wird die Wahrscheinlichkeit für das entsprechende Ergebnis notiert.
Pfade: Eine Folge von Ästen vom Startknoten bis zu einem Endknoten stellt ein mögliches Gesamtergebnis dar.

Beispiel: Zweimaliges Werfen einer Münze

Beim ersten Wurf kann Kopf (K) oder Zahl (Z) fallen, beim zweiten Wurf ebenso.

Die möglichen Pfade sind: K-K, K-Z, Z-K, Z-Z

Jeder Pfad hat die Wahrscheinlichkeit 0,5 · 0,5 = 0,25

Pfadregeln und Berechnung von Wahrscheinlichkeiten

Mit Baumdiagrammen können wir komplexe Wahrscheinlichkeiten durch zwei einfache Regeln berechnen.

Die Pfadregel (Multiplikationsregel)

Um die Wahrscheinlichkeit eines bestimmten Pfades zu berechnen, multipliziere die Wahrscheinlichkeiten entlang des Pfades.

$P(A \cap B) = P(A) \cdot P(B)$

Die Wahrscheinlichkeit, dass Ereignis A und danach Ereignis B eintritt, ist das Produkt aus den Wahrscheinlichkeiten für A und B. Bei mehrstufigen Zufallsexperimenten wird die Pfadregel angewendet, indem man die Wahrscheinlichkeiten entlang des Pfades multipliziert.

Die Summenregel (Additionsregel)

Um die Wahrscheinlichkeit für ein Ereignis zu berechnen, das durch mehrere Pfade erreicht werden kann, addiere die Wahrscheinlichkeiten dieser Pfade.

$P(\text{A oder B}) = P(\text{A}) + P(\text{B})$

Dies gilt für Ereignisse, die sich gegenseitig ausschließen (nicht gleichzeitig eintreten können).

Beispiel: Ziehen aus einer Urne

Eine Urne enthält 3 rote und 2 blaue Kugeln. Es werden nacheinander 2 Kugeln mit Zurücklegen gezogen.

Wie groß ist die Wahrscheinlichkeit, dass beide Kugeln rot sind?

$$P(\text{beide rot}) = P(\text{erste rot}) \cdot P(\text{zweite rot}) = \frac{3}{5} \cdot \frac{3}{5} = \frac{9}{25} = 0,36 = 36\%$$

Beispiel: Ziehen ohne Zurücklegen

Eine Urne enthält 3 rote und 2 blaue Kugeln. Es werden nacheinander 2 Kugeln ohne Zurücklegen gezogen.

Wie groß ist die Wahrscheinlichkeit, dass beide Kugeln rot sind?

$P(\text{beide rot}) = P(\text{erste rot}) \cdot P(\text{zweite rot}) = \frac{3}{5} \cdot \frac{2}{4} = \frac{3}{5} \cdot \frac{1}{2} = \frac{3}{10} = 0,3 = 30\%$

Nächste Schritte

Nachdem du die Grundlagen der Wahrscheinlichkeitsrechnung und Baumdiagramme kennengelernt hast, kannst du jetzt:

Interaktive Übungen bearbeiten, um dein Verständnis zu vertiefen
Spezifische Aufgaben zu Ziehen mit und ohne Zurücklegen lösen
Den Baumdiagramm-Generator ausprobieren, um eigene Wahrscheinlichkeitsprobleme zu visualisieren