Q
\(\Delta T\)
\(\Delta H\)

Energetik

Grundlagen der kalorimetrischen Messungen und Berechnungen für die 11. Klasse - Lerne, wie du Wärmeenergie berechnen und messen kannst.

1. Grundlagen der Wärmeenergie

In der Chemie spielt Energie eine zentrale Rolle. Bei chemischen Reaktionen wird Energie umgewandelt - entweder wird Energie freigesetzt (exotherme Reaktion) oder aufgenommen (endotherme Reaktion). In diesem Modul lernen wir, wie wir diese Wärmeenergie messen und berechnen können.

Exotherme Reaktionen

Bei exothermen Reaktionen wird Energie in Form von Wärme an die Umgebung abgegeben:

  • Die Temperatur der Umgebung steigt
  • Die Reaktionsprodukte haben eine geringere Energiemenge als die Ausgangsstoffe
  • Beispiele: Verbrennung, Neutralisation von Säuren und Basen

Endotherme Reaktionen

Bei endothermen Reaktionen wird Energie aus der Umgebung aufgenommen:

  • Die Temperatur der Umgebung sinkt
  • Die Reaktionsprodukte haben eine höhere Energiemenge als die Ausgangsstoffe
  • Beispiele: Fotosynthese, Auflösen von Ammoniumnitrat in Wasser

2. Berechnung der Wärmeenergie

Um die bei einer Reaktion freigesetzte oder aufgenommene Wärmeenergie zu berechnen, nutzen wir ein Verfahren namens Kalorimetrie. Wir werden die Temperaturänderung eines bekannten Wasservolumens messen, um die Wärmemenge zu bestimmen.

Die Grundformel zur Berechnung der Wärmeenergie:

\[ Q = m \cdot c \cdot \Delta T \]

wobei:

  • \(Q\) = Wärmeenergie in Joule (J)
  • \(m\) = Masse des Wassers in Kilogramm (kg)
  • \(c\) = spezifische Wärmekapazität von Wasser (4,184 J/(g·K) oder 4184 J/(kg·K))
  • \(\Delta T\) = Temperaturänderung in Kelvin (K) oder °C

Die spezifische Wärmekapazität

Die spezifische Wärmekapazität ist eine Stoffeigenschaft und gibt an, wie viel Energie nötig ist, um 1 Gramm eines Stoffes um 1 Kelvin (oder 1 °C) zu erwärmen. Wasser hat eine besonders hohe spezifische Wärmekapazität von 4,184 J/(g·K).

Stoff Spezifische Wärmekapazität
[J/(g·K)]
Wasser 4,184
Luft 1,005
Aluminium 0,897
Eisen 0,449
Gold 0,129

Temperaturanimation: Exotherme Reaktion

In dieser Animation kannst du beobachten, wie sich die Temperatur während einer exothermen Reaktion verändert. Die freigesetzte Wärmeenergie führt zu einem Temperaturanstieg im umgebenden Wasser.

3. Praktisches Experiment: Reaktion von Eisen mit Schwefel

Die Reaktion von Eisen mit Schwefel ist ein klassisches Beispiel für eine exotherme Reaktion. Bei dieser Reaktion verbinden sich Eisen und Schwefel zu Eisensulfid (FeS) und setzen dabei Wärme frei.

Reaktionsgleichung:

\[ \ce{Fe + S -> FeS} + \text{Wärme} \]

Versuchsaufbau

Benötigte Materialien:

  • Eisenpulver und Schwefelpulver im molaren Verhältnis 1:1
  • Ein Reagenzglas
  • Einen glühenden Nagel zum Starten der Reaktion
  • Ein Becherglas mit einer bekannten Menge Wasser
  • Ein Thermometer
  • Eine Waage
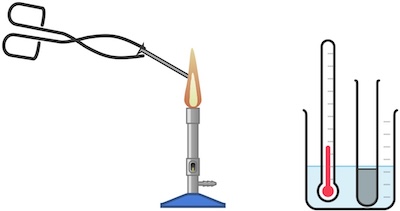
Versuchsaufbau: Eisen-Schwefel-Reaktion

Durchführung:

  1. Mische gleiche Massenteile Eisenpulver und Schwefelpulver und wiege die Gesamtmasse.
  2. Fülle die Mischung in ein Reagenzglas.
  3. Stelle das Reagenzglas in ein Becherglas mit einer bekannten Menge Wasser (z.B. 100 g).
  4. Miss die Anfangstemperatur des Wassers mit dem Thermometer.
  5. Erhitze einen Nagel und berühre mit dem glühenden Nagel die Mischung, um die Reaktion zu starten.
  6. Miss die Höchsttemperatur, die das Wasser erreicht.

Sicherheitshinweise

Diese Reaktion sollte nur unter Aufsicht einer Lehrperson durchgeführt werden! Es können giftige Schwefeldämpfe entstehen.

Schutzbrille und Handschuhe sind Pflicht!

Reaktionsanimation: Eisen-Schwefel-Reaktion

Diese Animation zeigt den Versuchsaufbau und den Ablauf der exothermen Reaktion zwischen Eisen und Schwefel.

4. Berechnung der Reaktionswärme - Ein Beispiel

Beispielrechnung:

Angenommen, wir haben folgende Messwerte:

  • Masse des Wassers: 100 g = 0,1 kg
  • Anfangstemperatur des Wassers: 22°C
  • Höchsttemperatur des Wassers nach der Reaktion: 27°C
  • Temperaturänderung \(\Delta T\): 5°C = 5 K
  • Spezifische Wärmekapazität von Wasser: 4,184 J/(g·K)

Berechnung der freigesetzten Wärmeenergie:

\[ Q = m \cdot c \cdot \Delta T \] \[ Q = 100\,\text{g} \cdot 4{,}184\,\text{J/(g·K)} \cdot 5\,\text{K} \] \[ Q = 2092\,\text{J} \approx 2{,}1\,\text{kJ} \]

Diese 2,1 kJ wurden bei der Reaktion freigesetzt und haben das Wasser erwärmt.

Eigene Berechnung

Probiere selbst, die Wärmeenergie für verschiedene Messwerte zu berechnen:

5. Weiterführende Überlegungen

Reaktionsenthalpie

Die molare Reaktionsenthalpie (\(\Delta H\)) gibt an, wie viel Energie bei einer Reaktion pro Mol umgesetzt wird. Sie ist eine wichtige Größe in der Thermodynamik und kann aus der gemessenen Wärmeenergie berechnet werden.

\[ \Delta H = \frac{Q}{n} \]

wobei \(n\) die Stoffmenge in Mol ist.

Vorzeichen der Reaktionsenthalpie:

  • Exotherme Reaktion: \(\Delta H < 0\) (negatives Vorzeichen), da Energie an die Umgebung abgegeben wird
  • Endotherme Reaktion: \(\Delta H > 0\) (positives Vorzeichen), da Energie aus der Umgebung aufgenommen wird

Bei der Eisen-Schwefel-Reaktion ist \(\Delta H\) negativ, da es sich um eine exotherme Reaktion handelt.

Wichtig

Das Vorzeichen der Reaktionsenthalpie ist eine Konvention in der Thermodynamik und hilft, den Energiefluss zu interpretieren. Es folgt dem Prinzip: Was das System abgibt (exotherm), wird negativ gezählt; was das System aufnimmt (endotherm), wird positiv gezählt.

Warum ist die Eisen-Schwefel-Reaktion exotherm?

Bei der Bildung von Eisensulfid (FeS) werden neue, stärkere chemische Bindungen zwischen Eisen- und Schwefelatomen gebildet. Die Bildung dieser Bindungen setzt Energie frei, die als Wärme abgegeben wird. Die Produkte haben eine geringere potentielle Energie als die Ausgangsstoffe.

Energie (kJ/mol) Reaktionsfortschritt 0 -100 ΔH = -100 kJ/mol Fe + S FeS Exotherme Reaktion Energie wird freigesetzt

Anwendungen in der Praxis

Das Verständnis von Energieumwandlungen bei chemischen Reaktionen ist fundamental für:

Entwicklung von Heizsystemen und Wärmekissen

Nutzung exothermer Reaktionen für Wärmegewinnung

Optimierung von Verbrennungsprozessen

Effiziente Energiegewinnung und Emissionsreduktion

Berechnung von Energiebilanzen

Planung und Kontrolle industrieller Prozesse

Verständnis biochemischer Prozesse

Stoffwechsel und Energiegewinnung im Körper

Entwicklung von Brennstoffzellen und Batterien

Nachhaltige Energiespeicherung und -umwandlung

6. Exotherme und endotherme Reaktionen im Vergleich

Exotherme Reaktionen

Definition: Energieabgabe an die Umgebung

Energiediagramm: Produkte haben niedrigere Energie als Edukte

Vorzeichen: \(\Delta H < 0\) (negativ)

Beispiele:

  • Verbrennung von Kraftstoffen
  • Reaktion von Metallen mit Sauerstoff (Oxidation)
  • Neutralisation von Säuren und Basen
  • Kondensation von Wasserdampf zu Wasser

Endotherme Reaktionen

Definition: Energieaufnahme aus der Umgebung

Energiediagramm: Produkte haben höhere Energie als Edukte

Vorzeichen: \(\Delta H > 0\) (positiv)

Beispiele:

  • Fotosynthese
  • Verdampfung von Wasser
  • Schmelzen von Eis
  • Thermische Zersetzung von Kalkstein

Anwendung: Kältekompresse

Ein alltägliches Beispiel für eine endotherme Reaktion ist die Kältekompresse:

Wenn Ammoniumnitrat in Wasser gelöst wird, nimmt es Wärme aus der Umgebung auf:

\[ \ce{NH4NO3 (s) + Wärme -> NH4+ (aq) + NO3- (aq)} \]

Diese Reaktion kann zur Kühlung bei Sportverletzungen verwendet werden, da die Temperatur der Kompresse sinkt.

7. Übungsaufgaben zur Wärmeenergie

Übungsaufgabe 1: Berechnungen zur Reaktionswärme

Bei der Verbrennung von 0,5 g Methanol (\(\ce{CH3OH}\)) in einem Kalorimeter mit 200 g Wasser steigt die Temperatur des Wassers von 22,0°C auf 27,5°C. Berechne:

  1. Die freigesetzte Wärmemenge in Joule
  2. Die molare Verbrennungsenthalpie von Methanol in kJ/mol (Molmasse von Methanol: 32 g/mol)

Übungsaufgabe 2: Energiebilanz

Eine 50 g schwere Metallprobe wird von 20°C auf 80°C erhitzt. Dabei werden 2300 J Energie aufgenommen. Berechne die spezifische Wärmekapazität des Metalls.